|
|
|
|
|
|
|
 |
|
Wer sich ein wenig mit fraktaler Geometrie
beschäftigt hat, der kennt das Sierpinski-
Dreieck. Denn im Zusammenhang mit dem
Pascalschen Dreieck hat dieses Fraktal
auch für die Zahlentheorie einiges zu bieten. |
Aber was passiert, wenn man diesen
Algorithmus auch auf andere regelmäßige
Vielecke loslässt?
Das Ergebis können Sie auf der rechten Abbildung "bewundern". Zugegeben, auf dem ersten Blick etwas langweilig. Wohl deshalb sind diese Fraktale bisher nur selten oder nie publiziert worden.
Dieser Sachverhalt wurde der Internetseite
von Moriz Lenz entnommen.
Was hier nun auffällt, ist das 5-Eck, welches tatsächlich noch fraktale Strukturen zeigt.
Nun gibt es etliche Möglichkeiten Fraktale zu errechnen, bei denen das 5-Eck (und nicht nur dieses) wesentlich deutlicher der allgemeinen Vorstellung von einem Fraktal entspricht:
|
|
|
 |
|
|
 |
|
|
Es gibt eine einfache und doch verblüffende Möglichkeit, ein Sierpinski-Dreieck (auch "Sierpinski-Sieb" genannt) mit dem Computer zu erstellen:
Man zeichnet ein gleichseitiges Dreieck und wählt zufällig einen beliebigen Punkt im Raum. Dann wählt man zufällig einen der Eckpunkte des Dreiecks, nimmt den Mittelpunkt zwischen dem letzten Punkt und dem gewählten Eckpunkt, und setzt einen neuen Punkt an diese Stelle.
Von dort aus wähle man wieder zufällig einen Eckpunkt, halbiert die Strecke, setzt dort einen Punkt hin und so weiter.
Nach 500 Iterationen (auch Rekursionsschritte genannt) kann man das Fraktal erkennen.
Nach 50000 Iterationen ist das Fraktal
bereits sehr detailiert zu erkennen.
|
|
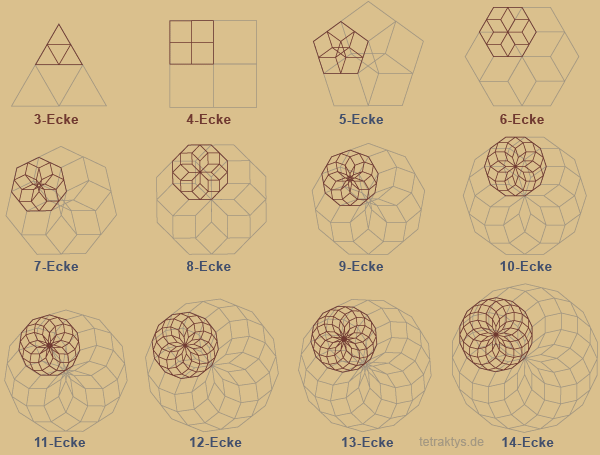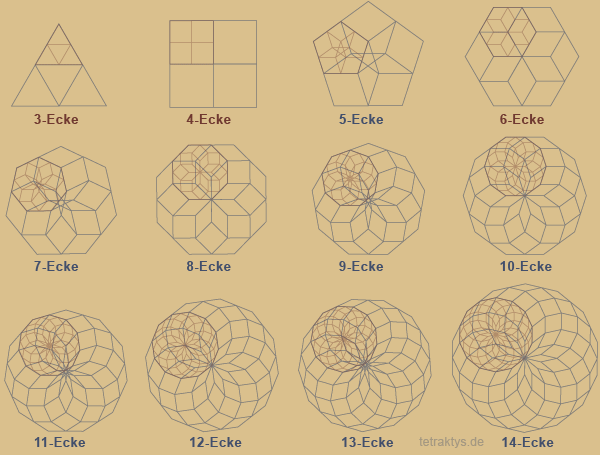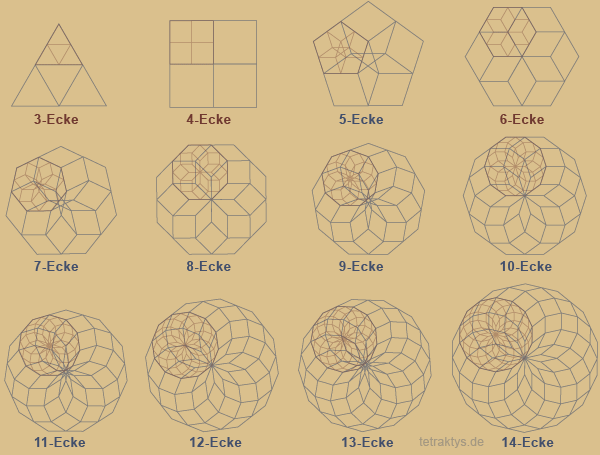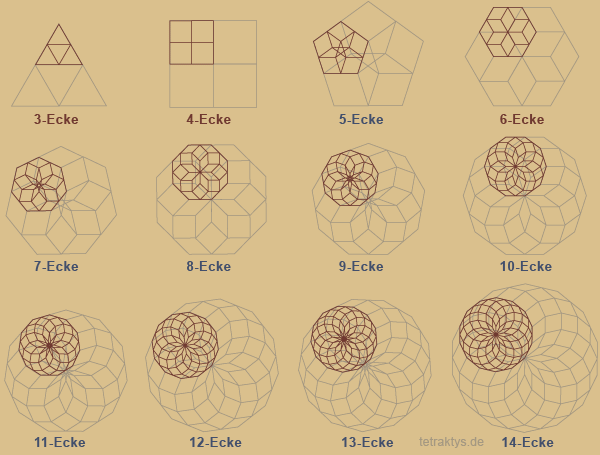
Wenn wir aber die Bedingungen für das Sierpinskidreieck, konsequent auch für andere Polygone einfordern:
1: Fraktale befinden sich im Vieleck selbst.
2.: Anzahl neu entstehender fraktaler n-Ecke
= Anzahl seiner Ecken.
2.: Die Seiten des n-Ecks halbieren sich in
jeder Iterationsstufe.
Dann müssen wir uns tatsächlich mit dem begnügen, was da rechts zu sehen ist.
Bei genauerer Betrachtung stellt man aber erfreulicherweise fest, dass diese Fraktale doch nicht so langweilig sind, wie der erste Eindruck glaubend macht. |
|
|
 |
|
|
|
|
|
 |
|
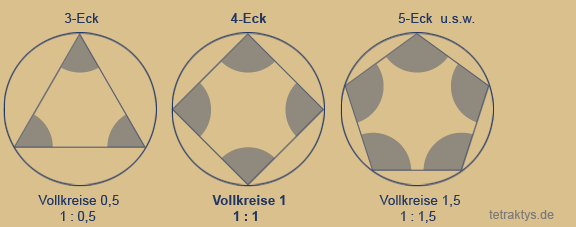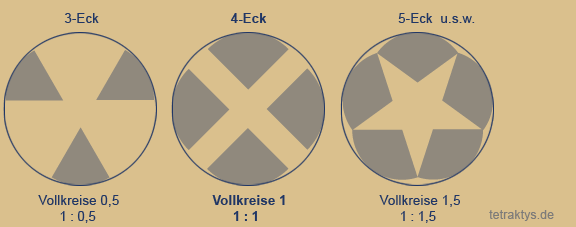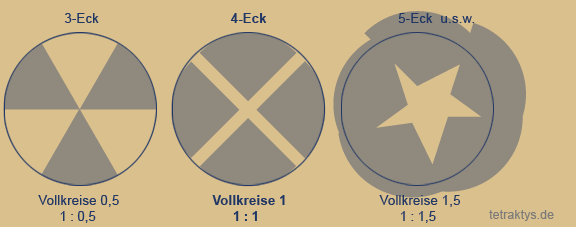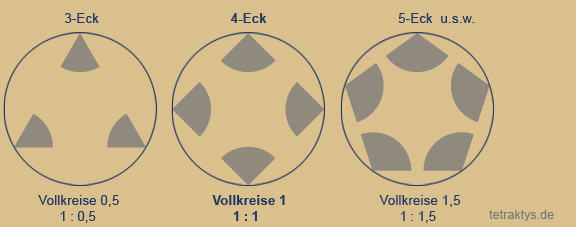
Da nun das Sierpinski-Dreieck in direkter Beziehung zum Pascalschen Dreieck steht und damit auch der Zahlentheorie verbunden ist, macht es also Sinn, auch auf andere Vielecke die gleichen Bedingungen für ein Fraktal anzuwenden.
Wenn diese Fraktale nicht als gefüllte Flächen dargestellt sind wie beim Sierpinski-Dreieck, sondern als Linienzeichnungen, dann wird die Architektur der Fraktale sichtbar!
Die rot animierte Figur zeigt ein Teil des Frakals in der nächsten Iterationsstufe. Diese Darstellung soll erst mal genügen, um das Prinzip zu zeigen, da mehrere vollständige Iterationsstufen eines Vielecks die Grafik "undurchschaubar" machen würden.
Zu den Details:
Beim Sierpinski-Dreieck sind die Fraktale bekanntlich so nebeneinander angeordnet, dass sich dazwischen entsprechende Leerräume bilden müssen.
Das Viereck mit seinen rechten Winkeln erlaubt keine Leerräume mehr. Denn alle Fraktale liegen Kante an Kante aneinander so, dass die Flächen eine Einheit bilden, wenn man sie mit Farbe füllen würde.
Beim 5-Eck passiert es:
Die Fraktale überlappen sich, und in der Mitte
entsteht ein Loch, genau wie beim Sierpinski-
Dreieck! Die nächste Iterationsstufe "stanzt nun
aus jedem der fünf vorangegangenen Fraktale
wieder jeweils ein Loch, immer ein um
180 Grad gedrehtes 5-Eck.
Diese Löcher entstehen nur bei ungeradzahligen Polygonen. Wenn man sich das genau anschaut und sich tiefer in diese Geometrie reindenkt, dann kann man diese Gesetzmäßigkeit nachvollziehen.
Ab dem 7-Eck nun erlauben die mehrfachen Überlappungen der Polygone dann auch keine
Löcher mehr im Zentrum der nächsten Iterationsstufen.
Es bleibt lediglich das Loch in der Mitte der ersten Iterationstufe von ungeradzahligen Vielecken, so wie ganz oben zu sehen ist.
Unten rechts noch einmal die Iterationsstufen
des 5-Ecks.
Links als Linienzeichnung, rechts parallel dazu die
mit Farbe gefüllte Figur. Um die Animation zu
beschleunigen, wurde gegen Ende auf Einzelschritte verzichtet. Diese Darstellung sollte aber reichen
um das Prinzip anschaulich zu machen.
|
|
 |
|
 |
|
|
Den gleichen Sachverhalt möchte ich noch einmal anders anschaulich machen:
Der Algorithmus welches das Sierpinski-Dreieck entstehen lässt, zwingt also das Quadrat und das Fünfeck in der Konsequenz zu dem, was die rechts stehende Animation zeigt.
Ab dem 5-Eck überlagern sich Fraktale.
Aus der entsprechenden Schnittmenge ergibt
sich ein Pentagramm! Das Pentagramm ist
der Grenzüberschreiter.
Das Ganze lässt sich aber auch noch anders darstellen, nämlich so wie die darunter stehende Animation es zeigt.
Mit diesem Sachverhalt treffen wir auch wieder
auf die Simplexe und die Zusammenhänge der Winkelsummen in Bezug auf die Tetraktys, siehe:
SIMPLEX – DREIECKSZAHLEN
& DEZIMALCODIERUNG
Wenn man nun beide Darstellungen
aufmerksam betrachtet und wirklich ernsthaft
über diese Zusammenhänge nachdenkt,
dann muss man zu dem Schluss kommen,
dass das Quadrat mit dem Einheitskreis
in einer direkten Wechselbeziehung steht!
Die Ursache sind die vier Innenwinkel von
je 90 Grad, die zusammen den Einheitskreis
ergeben.
Die Konsequenz dieser Einsicht:
Die Pythagoreische Tetraktys steht
für Einheit und Vollständigkeit!
|
|
|
|
|
|
 |
|
 |
|
 |
|
|
Der hier dargestellte Sachverhalt beschreibt eigentlich schon das Wesen der Tetraktys: Dreieck und Quadrat bilden auch jene fraktalen Strukturen, die wir auch in der flächenfüllenden und raumfüllenden Parkettierung von Polygonen und Polyedern im Zusammenhang mit Kristallgittern
von Kugelpackungen antreffen.
Ab dem 5-Eck überlappen sich die Polygone.
Die Ziffer 5 ist der Grenzüberschreiter des Raumes.
Im Folgenden möchte ich aber speziell auf
eine interessante Entsprechung zur Pythagoreischen Tetraktys hinweisen,
die sich direkt als
1 + 2 + 3 + 4 = 10
ausdrückt, und die sich ihrem Wesen nach
genau so, auch in anderen Symmetrien
manifestiert!
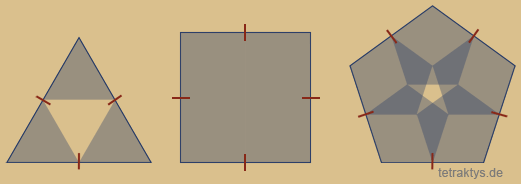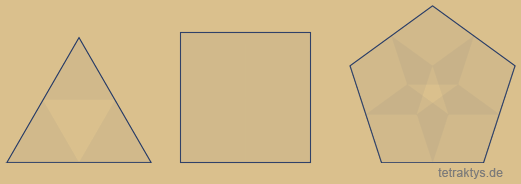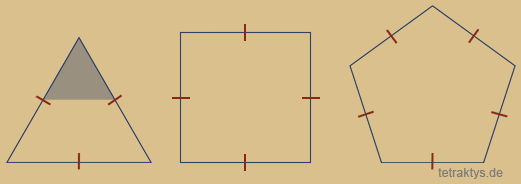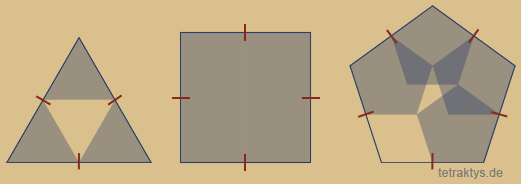
In den folgenden Abbildungen sind die Flächen alternierend, also abwechselnd mit Farbe gefüllt, um die Überschneidungen der Vielecke besser sichtbar zu machen. Theoretisch würde es aber reichen, diese als Umrisse (Linien) darzustellen. Es würde an der Sache nichts ändern.
Die erste Animation rechts zeigt nun das Sierpinski-Dreieck nur in seiner ersten Iterationsstufe.
Was sich nun in dieser Animation ändert,
sind lediglich die Ecken des Polygons!
Wir sehen also eine Abfolge von "Sierpinski-Vielecken" in der ersten Iterationsstufe!
Das Dreieck entspricht noch dem Sierpinski-Dreieck. Wendet man oben stehende Bedingungen auf das Quadat an, haben wir folgerichtig einfach
ein Quadrat mit doppelter Kantenlänge, da ja
das Quadrat in der Ebene mit sich selbst
parkettierbar ist.
|
|
Ab dem 5-Eck aber müssen sich nun zwangsläufig die Fraktale überschneiden, in der Art, dass sie sich um einen zentralen Punkt gruppieren! Das Viereck mit seinen rechten Winkeln ist das letzte Fraktal, in dem keine Überschneidungen entstehen.
Aber wir wollen hier einem anderen interessanten Sachverhalt Beachtung schenken, weshalb uns das 10-Eck interessiert. Dazu betrachten wir uns die rechts stehende Animation:
So wie sich das Sierpinskidreieck der ersten Iterationsstufe in 3 Dreiecke zergliedert,
teilt sich auch das fraktale Zehneck der ersten Iterationsstufe in 10 10-Ecke, welche sich aber
nun überlagern.
|
|
Auf Grund der Überlagerungen entstehen 40 Vierecke in diesem Fraktal. Jedes von diesen 10
10-Ecken beinhaltet jeweils 10 Vierecke!
10-Eck = 10 Vierecke!
Kleinere n-Eck-Fraktale beinhalten weniger Vierecke als die Anzahl ihrer Ecken,
größere n-Eck-Fraktale beinhalten mehr Vierecke als die Anzahl ihrer Ecken!
Und natürlich haben wir auch hier wieder die klare Gliederung der Tetraktys in der Weise, wie die 10 Vierecke im 10-Eck angeordnet sind: Von der Peripherie des 10-Ecks bis zum Mittelpunkt in dieser Reihenfolge: 1 + 2 + 3 + 4 = 10 !
|
|
|
|
 |
|
|
|
 |
|
|
|
Das Sierpinskidreieck
in der ersten Iterationsstufe,
angewandt auf höhere n-Ecke
in diesem Fall bis zum 14-Eck.
|
|
|
Die Überschneidungen der benachbarten
10-Ecke ergeben genau 10 Vierecke.
n-Ecke < 10 haben weniger Vierecke.
n-Ecke > 10 haben mehr Vierecke.
|
|
 |
|
|
|
|
|
|
|
 |
|
Auch die Geometrie der Simplexe bestätigt
mit ihren 4 Grundtypen der Sternpolygone
in ganz direkter Weise diesen
zahlentheoretischen Zusammenhang:
|
|
Warum könnte das interessant sein?
Wir stoßen hier auf eine Gesetzmäßigkeit,
die wir nicht nur in diesem Beispiel antreffen!
Um sich einen Überblick zu verschaffen, schauen Sie bitte hier!
In dieser Geometrie sind mit Sicherheit ebenso
viele wichtige Informationen verborgen, die Licht
in das Dunkel der Zahlentheorie bzw. der
Primzahlverteilung bringen können, wie dies auch
in der Geometrie der Simplexe der Fall ist.
Deshalb möchte ich noch einmal darauf hinweisen, dass diejenigen Fraktale, die sich mit ihrem besonderen Erscheinungsbild von den restlichen n-Ecken bis in den unendlichen Zahlenraum abheben, eben auch in der Primzahlproblematik "federführend" sind.
Das 3-Eck und das 5-Eck!
Siehe die schon oben gezeigte Abbildung
hier noch einmal ganz rechts zu sehen!
Die Ziffer 3 "erzeugt" mit dem Sieb des
Eratosthenes den 6er-Takt der Primzahl-
zwillingsbildung, wogegen die Ziffer 5 diese Ordnung wieder "zerhackstückt".
|
|
 |
|
|
Leider habe ich noch keine Zeit gefunden, dieses überaus interessante und wichtige Thema "fraktale Vielecke" weiter zu vertiefen.
Sollten Sie eine spezielle Frage oder einen anregenden Hinweis zu diesem Thema haben,
so schreiben Sie uns einfach eine Email an:
info@tetraktys punkt de
(Das Wort "punkt" bitte mit . ersetzen.)
Bitte schauen Sie hin und wieder
mal hier vorbei.
^ Zurück nach oben zum Menü ^
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|