|
|
|
1 + 2 + 3 + 4 = 10 – was soll man damit anfangen?
Egal welche Quellen man bemüht, nirgends kann man herauslesen, dass diese "Tetraktys" etwas konkretes bzw. sinnvolles in der Mathematik darstellt. Das allgemein bekannte Symbol der pythagoreischen Tetraktys kommt in der Gestalt eines 10-Punkte-Dreiecks daher:
|
|
1 Punkt,
3 Punkte (1+2),
6 Punkte (1+2+3),
10 Punkte (1+2+3+4),
15 Punkte (1+2+3+4+5) usw...
Die Ziffer 10 ist also die vierte Dreieckszahl!
Aber was macht die Zahl 10 so besonders?
Warum hat Pythagoras sowohl die Zahl 4
als auch die Zahl 10 regelrecht "vergöttert"?
Aus einer Laune oder einer religiösen Überzeugung heraus? Oder irrte er ganz einfach?
Das Widersprüchliche daran ist, dass ja
Pythagoras durchaus konstruktive Mathe in die Welt gesetzt hat. Warum also gerade 10?
|
|
Zur Zahl 10 fällt uns natürlich als erstes unser Dezimalsystem ein. Hat also unser Zählsystem etwas mit dieser Tetraktys zu tun? Zumindest wird das im allgemeinen gern behauptet.
Die Antwort ist ein absolutes "NEIN" für alle selbständig denkenden Menschen, die sich wirklich intensiv mit den hier gezeigten geometrisch-zahlentheoretischen Zusammenhängen beschäftigt haben.
Die Zahl 10 im Zusammenhang mit der
pythagoreischen Tetraktys hat > keinen <
Sonderstatus, der aus dem menschlichen
Geist resultiert!
Die Tetraktys ist kein menschliches Konstrukt, sondern die Konsequenz, die sich aus der Folge der natürlichen Zahlen und der entsprechenden Geometrie ergibt!
Betrachten wir uns zuerst einfach mal eine interessante Eigenschaft der Dreieckszahlen, die einen ersten Einblick in das Wesen der Tetraktys zulassen.
Dazu im Folgenden drei Beispiele:
|
|
|
|
 |
|
|
|
Das 10-Punktedreieck hat eine Kantenlänge von jeweils 4 Punkten. Diese Punktedreiecke nennt man in der Mathematik "figurierte Dreieckzahlen". Die Folge der Dreieckzahlen wird mit der schrittweisen Vergrößerung dieser Punktedreiecke dargestellt:
|
|
|
|
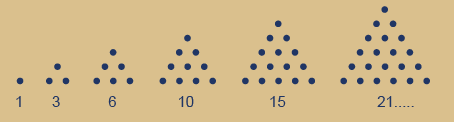 |
|
|
|
 |
|
|
Beispiel Nr. 1:
Zuerst das Punktedreieck selbst, welches z.B. auch dem hexagonalen Gitter in der Kristallographie zugeordnet ist. Diese Thematik wird hier demnächst ohnehin noch eine größere Rolle spielen.
Zu sehen ist hier also, dass die aufkumulierte Menge (Gesamtpunktemenge) vor dem
10-Punkte-Dreieck ebenfalls = 10 ist.
Hier gibt es sozusagen einen Punktegleichstand:
10 = 10 !
Bei der Zahl 10 geht die Schere auseinander, eine Zahlenreihe überholt die andere: |
|
In Zahlen ausgedrückt sieht das dann folgendermaßen aus:
Links die Dreieckszahlen, rechts die aufkumulierte Menge >vor< der jeweiligen Dreieckszahl:
|
|
Dann haben wir folgende Verhältnisse: |
|
|
|
1
3
6
10
15
21
|
=
<
<
<
<
<
|
1
4
10
20
35
46
|
|
|
|
1
3
6
10
15
21
|
>
>
>
=
<
<
|
0
1
4
10
20
35
|
|
|
|
Wir haben dann der Dreieckszahl 6 die aufkumulierte Menge 10 gegenüberstehend!
Der Dreieckszahl 10 dagegen steht die Menge 20, also die genau doppelte Menge gegenüber. Auch mit dieser Besonderheit ist die Zahl 10 die einzige Dreieckszahl!
Dass die Gegenüberstellung der Zahl 6 und 10 ebenfalls sehr interessant ist, werden wir uns noch in vielfacher Weise eindrucksvoll vor Augen führen!
Aber bleiben wir mal bei der ersten Variante. Für sich gesehen noch nichts spektakuläres, wenn diese Tatsache nicht mit Geometrie verknüpft wäre, die eine völlig andere ist!
Aber auch wenn man die selbe Struktur im dreidimensionalen Raum (Kugelpackungen und ihre Kristallgitter) betrachtet, auch dann trifft man wieder auf gleiche Gesetzmäßigkeiten.
|
|
|
|
Natürlich könnte man sagen, dass diese nur eine Sichtweise ist, denn die aufkumulierte Menge kann auch die Zahl, der sie gegenübergestellt wird, beinhalten. |
|
|
|
 |
|
|
|
 |
|
|
 |
|
|
|
Beispiel Nr. 2:
Betrifft die Geometrie der Simplexe, welche man blumig formuliert, als einen anderen Agregatzustand der Zahlen bezeichnen kann, besonders dann, wenn man diese in einem Koordinatensystem auffächert und die einzelnen Sternpolygone untersucht.
Mit Hilfe der Geometie der Simplex hat man wahrhaftig die Möglichkeit, aus unserem Dezimalsystem herauszutreten! Das Dezimalsystem in dem wir rechnen, denken und leben! Wer kann spontan in einem anderen Zählsystem im Kopf multiplizieren oder dividieren? Wer das schafft der hat einen IQ von 250 oder mehr.
Was ich damit sagen will: Wir (und auch alle Mathematiker) können den Wald vor lauter Bäumen nicht sehen, wenn wir nur mit Zahlen operieren, ohne die analoge Geometrie zu Hilfe zu nehmen.
Alles baut sich auf dem Dezimalsystem auf, von dem gesagt wird es wäre nur deshalb in Gebrauch, weil wir seit jeher üblicherweise mit zehn Fingern abzählen. Das mag vielleicht tatsächlich so sein. Es gibt keinen "Gegenbeweis".
Aber: Zählt die Geometrie der Simplexe (Polygone und Sternpolygone) auch mit zehn Fingern?
Die erstaunliche Antwort lautet: JA!
|
|
Sie zählt sogar mit zwei Händen zu je fünf Fingern. Dass mit Hilfe der Geometrie der Simplexe das determinierende System der Primzahlverteilung offenbar wird, ist besonders interessant, da hiermit die unmittelbare Verknüpfung zwischen Zahlentheorie und der Geometrie von Kreisen und Kugeln – also der Symmetrie – offenbar wird.
Wo aber steckt in den Simplexen dieses
1 + 2 + 3 + 4 = 10 ?
Nun, es gibt nur ein Simplex, für welches gilt:
n-Eck = Vollkreise.
Es ist das 10-Eck-Simplex!
Das 10-Eck-Simplex hat in der Summe 10 Vollkreise. Gemeint ist die Summe aller eingezeichneten Sternpolygone inklusive das Polygon (10-Eck) selbst.
Vollkreise = Summe aller Innenwinkel der Peripherie vom Polygon und eingezeichneten Sternpolygonen. Eine genaue Erläuterung dazu finden Sie hier: tetraktys 1.pdf
Beim 10-Eck-Simplex geht wieder die Schere auseinander, genau wie beim Punktedreieck.
Simplexe < 10 haben weniger Vollkreise,
Simplexe > 10 haben mehr Vollkreise.
|
|
|
|
Und wie man an Hand dieser Animation sehr schön sehen kann, spiegelt sich in dieser Geometrie die Tetraktys der Pythagoreer korrekt wieder in diesen 1 + 2 + 3 + 4 = 10.
Zu diesem Tatbestand hier noch einmal die detailierte Zeichung: tetraktys 1.pdf
|
|
|
|
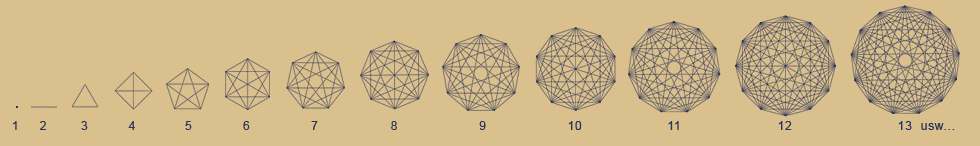 |
|
|
 |
|
|
|
|
|
|
|
Beispiel Nr. 3:
Wer sich ein wenig mit fraktaler Geometrie beschäftigt hat, der kennt das Sierpinskidreieck.
Für den Zahlentheoretiker hat dieses Fraktal die allergrößte Bedeutung, wenn man nur an das Pascalsche Dreieck denkt.
Fast überhaupt nicht bekannt und selten publiziert werden dagegen n-Ecke als fraktale Strukturen, die sich vom Sierpinskidreieck direkt konsequent abgeleiten lassen.
Dies sind die Bedingungen:
1: Fraktale befinden sich im Vieleck selbst.
2.: Anzahl neu entstehender fraktaler n-Ecke
= Anzahl seiner Ecken.
2.: Die Seiten des n-Ecks halbieren sich in
jeder Iterationsstufe.
Hier wird dieser Sachverhalt ausführlicher beschrieben
Der Übersichtlichkeit halber bleiben wir bei der ersten Iterationstufe. (Iterationsstufe = eine Stufe fraktaler Zergliederung).
|
|
Welche Geometrie entsteht, wenn sich die Anzahl der Ecken des Polygons (des Dreiecks) erhöht?
Betrachten Sie dazu die Animation in der Mitte.
Achtung! Es handelt sich hier nicht mehr um eine Abfolge von Iterationsstufen! Nur die Anzahl der Ecken innerhalb der ersten Iterationsstufe erhöht sich.
Das Dreieck entspricht noch dem Sierpinski-Dreieck. Wenn man oben stehende Bedingungen auf das Quadat anwendet, dann haben wir folgerichtig einfach ein Quadrat mit doppelter Kantenlänge, da ja das Quadrat in der Ebene mit sich selbst pflasterbar ist.
Ab dem 5-Eck aber müssen sich nun zwangsläufig die Fraktale überschneiden, in der Art, dass sie sich um einen zentralen Punkt gruppieren! Hier wären wir schon mitten drin in den geometrischen Grundlagen, welche die Tetraktys ausmachen. Das Viereck mit seinen rechten Winkeln ist das letzte Fraktal, in dem keine Überschneidungen entstehen. Ein großes Thema für sich.
Aber wir wollen ja Beispiel Nr. 3 untersuchen, weshalb uns das 10-Eck interessiert.
|
|
Dazu betrachten wir uns die letzte Animation ganz rechts. So wie sich das Sierpinskidreieck der ersten Iterationsstufe in 3 Dreiecke zergliedert,
teilt sich auch das fraktale Zehneck der ersten Iterationsstufe in 10 10-Ecke, welche sich aber
nun überlagern.
Auf Grund der Überlagerungen entstehen 40 Vierecke in diesem Fraktal. Eines von diesen 10
10-Ecken beinhaltet jeweils 10 Vierecke!
10-Eck = 10 Vierecke!
Kleinere n-Eck-Fraktale beinhalten weniger Vierecke als die Anzahl ihrer Ecken,
größere n-Eck-Fraktale beinhalten mehr Vierecke als die Anzahl ihrer Ecken!
Also auch in diesem dritten Beispiel geht bei der Zahl 10 die Schere auseinander.
Und natürlich haben wir auch hier wieder die klare Gliederung der Tetraktys in der Weise, wie die 10 Vierecke im 10-Eck angeordnet sind: Von der Peripherie des 10-Ecks bis zum Mittelpunkt in dieser Reihenfolge: 1 + 2 + 3 + 4 = 10 !
|
|
|
|
 |
|
 |
|
|
|
 |
|
|
|
Das Sierpinskidreieck
als Paradebeispiel für ein Fraktal.
|
|
|
Das Sierpinskidreieck
in der ersten Iterationsstufe,
angewandt auf höhere n-Ecke
in diesem Fall bis zum 14-Eck.
|
|
|
|
|
Die Überschneidungen der benachbarten
10-Ecke ergeben genau 10 Vierecke.
n-Ecke < 10 haben weniger Vierecke.
n-Ecke > 10 haben mehr Vierecke.
Interessant dabei:
Es sind >6< der benachbarten 10-Ecke, welche die Überschneidungen erzeugen!
Siehe Ausführungen weiter unten.
|
|
|
|
Da sich die Fraktale ab dem 5-Eck überschneiden, ist bei gefüllten Flächen normalerweise keine Strukur mehr erkennbar, es sei denn, man füllt die Flächen der Überschneidungen alternierend wie hier dargestellt, oder man zeichnet nur die Umrisse. Zur Veranschaulichung des Problems
hier ein externer Link . Nach dem Öffnen des Links schaue man im unteren Bereich dieser Webseite.
|
|
|
|
 |
|
|
|
Das 10-Punktedreieck, Kreisgeometrie
und des Sieb des Eratosthenes
Was könnte hinter diesen geometrischen Gesetzmäßigkeiten stecken? In allen drei Beispielen ist die Grundlage der "auseinander gehenden Schere" die Abfolge der Dreieckszahlen, so wie sie das Punktedreieck präsentiert. Also:
1, 3, 6, 10, 15, 21, 28 usw...
Das heist also: wenn die Punktedreiecke figurierte Dreieckszahlen verkörpern, dann trifft das für die zwei weiteren Beispiele ebenfalls zu!
Um den roten Faden von 1+2+3+4=10 nicht zu verlieren, habe ich hier eine zweite wichtige Besonderzeit der Punktedreiecke noch nicht gezeigt!
|
|
Die Ziffer 3 bzw. 6 ist eigentlich die erste,
bei der die "Schere auseinander geht". Betrachten Sie dazu die unten links stehende Grafik:
Das waren sicher Sachverhalte, die Pythagoras seinen Schülern mit den Zählsteinen zeigen wollte...
Aber was steckt dahinter?
Könnte es sein, dass die Pythagoreer
nicht nur eine kindliche Freude an Dreiecks-
zahlen oder Quadratzahlen hatten sondern,
dass sie mit dem 10-Punktedreieck etwas
wirklich Bedeutendes entdeckt hatten?
Etwas, von dem ihre Seele so beeindruckt war, dass es religiöse Gefühle erzeugte ?
|
|
Ist vielleicht dieses schlichte Punktedreieck der heilige Gral der Primzahlproblematik, den sie dann "Tetraktys" nannten?
Nur eine vage Vermutung?
Ganz sicher nicht!
Denn genau genommen ist das Sieb des Eratosthenes eine Abfolge regelmäßiger, sich überlagernder Punkteraster – im Lambdoma!
Es handelt sich dabei also nicht nur um figurierte Zahlen, sondern um figurierte Zahlenbrüche, dargestellt in einem entsprechenden Koordinatensystem,
in welchem sich beispielsweise auch die
n-Simplexe auffächern lassen!
Lesen Sie dazu:
DAS LAMBDOMA – MATRIX DER SCHÖPFUNG?
|
|
|
 |
|
|
|
 |
|
|
Innerhalb des 6-Punkte-Dreiecks haben wir ebenfalls einen "Punke-Gleichstand". Zu drei Punkten kommen drei Punkte hinzu.
|
|
Als Gegenüberstellung noch einmal den Punktegleichstand der 10.
Die aufkumulierte Menge vor dem 10-Punktedreieck ist 10. 10 = 10
|
|
Lesen Sie zur Bedeutung der Ziffer 5 bzw. 10
im Zusammenhang mit der Primzahlverteilung:
TETRAKTYS PART 2 – DIE "UNORDNUNG" DER PRIMZAHLEN
Die Ziffer 5 erzeugt als Punkteraster (Sieb des Erathostenes im Koordinatensystem von Zähler und Nenner) den Ausfall der Primzahlen = unregelmäßige Primzahlverteilung ab der Ziffer 25, also 5 x 5
Das Pentagramm = 2,5 x 10
Religionsphilosophisch: "Der Sündenfall" oder "Sturz in die Materie"
|
|
Lesen Sie zur Bedeutung der Ziffer 3 bzw. 6
im Zusammenhang mit der Primzahlverteilung:
TETRAKTYS PART 1 – DIE ORDNUNG DER PRIMZAHLEN
Die Ziffer 3 erzeugt als Punkteraster (Sieb des Erathostenes im Koordinatensystem von Zähler und Nenner) den 6er Takt, innerhalb welchem die Zwillingsbildung der Primzahlen begründet ist.
Das Dreieck zum 6-Stern
Religionsphilosophisch: "Die Schöpfung in 6 Tagen."
|
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
 |
 |
|
|
|
 |
|
|
^ Zurück nach oben ^
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|