|
|
|
|
|
|
|
 |
|
Es sind naturgemäß die einfachsten Formen,
deren Symbolkraft in der Menschheits-
geschichte immer schon eine große kultur-
historische Bedeutung zukam:
Kreis, Dreieck und Quadrat.
Auf dem ersten Blick drei geometrisch scheinbar
gegensätzliche Figuren. In Wahrheit ergänzen sich die Symbole, deren mythologische Bedeutung bis auf biblische Zeiten zurückgeht.
Der Kreis führt in sich selbst zurück, steht daher
für die Einheit, die Vollkommenheit oder auch
Klarheit.
Als unendliche Linie symbolisiert er
auch die Unendlichkeit. Mit einem Punkt in der Mitte wird er zum Symbol der Schöpfung.
Im Zen-Buddhismus symbolisieren Kreise die
höchste Stufe der Erleuchtung, die Harmonie
aller geistigen Kräfte.
|
|
geometrische Form und steht daher vor allem für
Stabilität im physischen Sinn, im metaphysischen
Sinn zusätzlich auch für Energie = männlich.
Das Quadrat symbolisiert die irdische Existenz, statische Perfektion und Integration. Es verkörpert die Materie = weiblich.
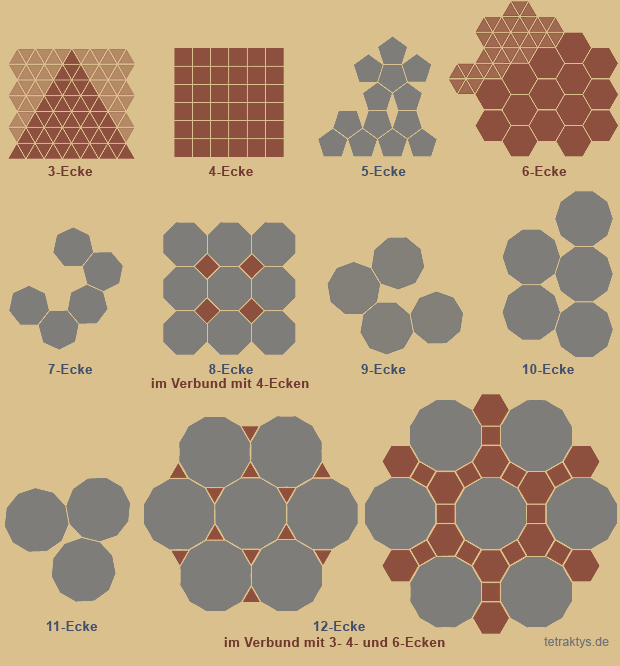
Wenn man nun natürliche Zahlen in einer Reihe nebeneinander als Polygone darstellt, so wie oben
zu sehen ist, dann fällt auf, dass eben genau
die ersten Polygone, diejenigen mit dem prägnantesten Erscheinungsbild sind.
Denn irgendwo ab dem 10-Eck werden die Ecken immer undeutlicher erkennbar, die Kontur des Polygons nimmt zunehmend die Kreisform an.
Allerdings:
genau diejenigen Polygone, die am weitesten von der Kreisform entfernt sind – nämlich
Dreieck und Quadrat – stehen mit dem
Kreis in einer unmittelbaren und direkten
Wechselbeziehung.
Weiter unten wird das verdeutlicht.
|
|
In der nun folgeden Betrachtung möchte
ich den Leser dazu ermuntern, trivialste
Geometrie und ihre Entsprechung in der
Zahlentheorie tiefer auf das Bewusstsein
wirken zu lassen.
Außerdem wird hier auf dieser Internetseite auch
auf die exakte arithmetische Entsprechung der
Simplexe (Polygone mit eingezeichneten
Tangenten) eingegangen.
Dabei wird klar, dass grundlegende Prinzipien in
der Zahlentheorie sich eben auch in diesen
geometrischen Entsprechungen manifestieren,
um sich dann bis unendlich zu wiederholen.
Bekannte Beispiele sind:
die geraden und ungeraden Zahlen, oder die Zwillingsbildung der Primzahlen im 6er Takt.
Wie insbesondere auch die Ziffern 3, 4 und 5
in direkter Weise auf die Primzahl-
problematik einwirken, wird unter der Rubrik
Zahlentheorie erläutert.
Denn letztendlich geht es hier ja um: Zahlentheorie + Geometrie = Philosophie.
|
|
|
|
 |
|
Das Dreieck widerspiegelt die dreifältige Natur des
Universums, These, Antithese, Synthese oder Vater, Mutter, Kind.
Von jeher gilt die Zahl drei als mystische Zahl.
Das gleichseitige Dreieck ist die stabilste
|
|
 |
|
|
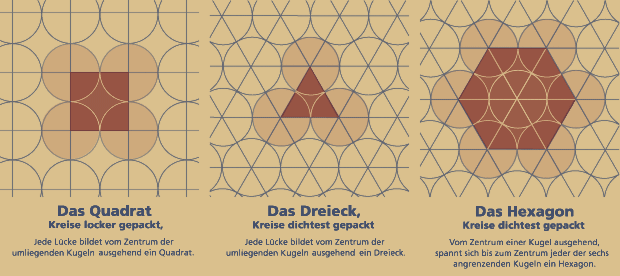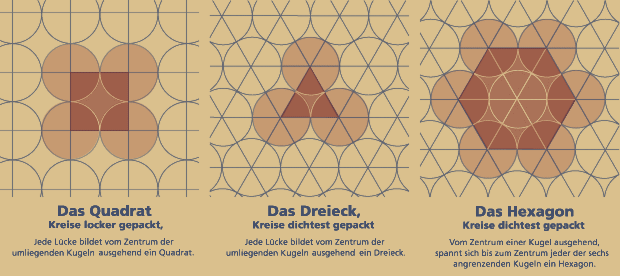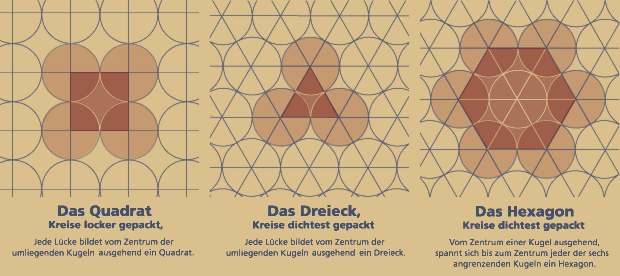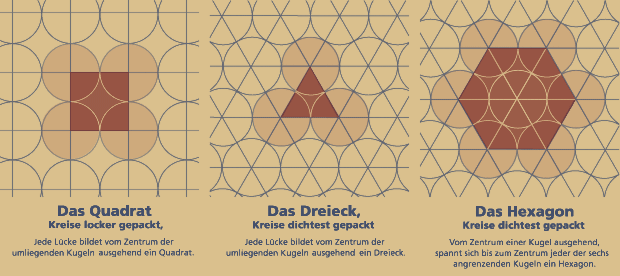
Parkettierung von regulären Polygonen
(Platonische und Archimedische Parkettierungen)
Wenn wir uns zahlentheoretischen Entsprechungen annähern wollen, dann müssen wir Symmetrien zugrunde legen, also Polygone, die gleiche Seiten und gleiche Innenwinkel haben. Diese werden regelmäßige bzw. reguläre Polygone genannt.
Das was auf der rechten Abbildung zu sehen ist scheint völlig unspektakulär und banal zu sein, in jeder Fliesenausstellung eines Baumarktes kann man sich ähnliches betrachten.
Gerade deshalb empfiehlt es sich, diese
Zusammenhänge bewusster vor Augen zu
führen.
Ist also nur ein regelmäßiges n-Eck als Kachel zugelassen und wird weiter eingeschränkt, dass
die Kacheln Kante an Kante angeordnet werden müssen, ergeben sich genau drei mögliche Parkettierungen der Ebene, die:
Platonischen Parkettierungen, auch regelmäßige Parkettierungen genannt.
Es sind nur Dreieck, Quadrat und Sechseck, welche diese Anforderung erfüllen können.
Alle anderen gleichseitigen Polygone sind
nicht lückenlos mit sich selbst parkettierbar.
Das Sechseck stellt zusätzlich noch einen Sonderfall dar:
Es ist überhaupt das einzige regelmäßige Polygon, welches sich aus einem anderen
Polygon, nämlich dem Dreieck zusammen-
setzt!
Und genau das sind die Hinweise zu den
Entsprechungen in der Zahlentheorie.
Auffällig ist weiter, dass das 5-Eck genau zwischen zwei parkettierbaren Polygonen rangiert. Es ist das erste Polygon, welches nicht mit sich selbst parkettierbar ist.
Auch das 7-Eck als 2. nicht parkettierbares Polygon hat eine ähnliche Positionierung, wenn man die ganz spezielle Besonderheit
des 8-Ecks betrachtet, nämlich, dass sich
die Lücken mit Quadraten füllen lassen.
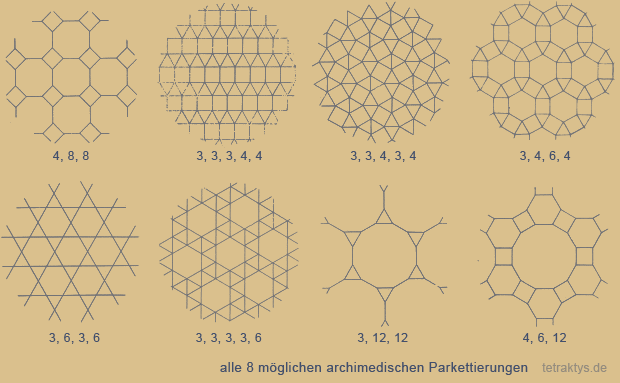
In diesem Fall spricht man von einer: semiregulären oder Archimedischen Parkettierung.
Das letzte reguläre Polygon welches eine
solche Option zulässt ist das 12-Eck,
wahlweise mit Dreiecken oder Quadraten
und Sechsecken.
Alle weiteren Polygone ab dem 13-Eck sind weder mit sich selbst noch mit anderen regulären Polygonen parkettierbar, da sie mit zunehmender Größe die Kreisform annehmen. Dieses Phänomen wird Kristallographische Restriktion genannt.
Symmetriegruppem periodischer Parkettierungen können nur Drehungen um 360°, 180°, 120°, 90° und/oder 60° enthalten.
Es handelt sich also um Elemente der Ordnungen 1, 2, 3, 4 und 6. Jedoch keine Drehungen um andere Winkel, also keine Elemente der Ordnungen 5, 7 oder höher.
Dieser Sachverhalt gilt auch für „reale“
Kristalle im dreidimensionalen Raum.
Siehe nächste Rubrik:
DIE GEOMETRIE DER LÜCKENLOSEN RAUMFÜLLUNG
Die Ordnung 5 ist jedoch bei Quasikristallen möglich, die eine „fast“ periodische Teilung haben.
Schauen wir uns nun arithmetische Entsprechungen analog zur Parkettierbarkeit
dieser ersten regulären Polygone an:
3- und 6-Eck – mit sich selbst parkettierbar:
Das Sechseck ist außerdem das einzige regelmäßige Polygon, welches sich aus einem anderen Polygon, nämlich dem Dreieck zusammensetzt!
Die Parallele zur Zahlentheorie:
Die Ziffer 3 stellt mit dem Sieb des Eratosthenes den 6er-Takt, innerhalb dessen sich alle Primzahlen bis unendlich ordnen.
Primzahlen stehen in Zwillingen um die dreiteilbar geraden – also 6-teilbaren Zahlen.
Analog zur Dualität gerader und ungerader Zahlen: Dreiecke lassen sich nur im Wechsel aufrecht und gestürzt pflastern.
4-Eck – mit sich selbst parkettierbar:
Die Ziffer 4 steht für das viergliedrig, fraktale und allumfassende Ordnungsgefüge, welches u.a. im Zusammenhang mit der unregel-
mäßigen Primzahlverteilung auf dieser Internetseite als "Pythagoreische Tetraktys" beschrieben wird.
Das 4-Eck ist das einzige Polygon mit der Innenwinkelsumme von einem vollen Kreis.
Der volle Kreis steht als Symbol für eine in sich abgeschlossene Ordnung.
|
|
 |
|
 |
|
5- und 7-Eck – nicht parkettierbar:
Die Ziffer 5 ist die erste Primzahl innerhalb des 6er Taktes, ihr Zwilling ist die 7. Die 5 ist jene Zahl, die mit der unregelmäßigen Primzahlverteilung direkt nach der Ziffer 24 (5x5) zu tun hat. Siehe:
TETRAKTYS PART 2
– DIE "UNORDNUNG" DER PRIMZAHLEN
Die Ziffer 5 durchbricht eine bestehende Tetraktys, sie steht für Chaos und Neuordnung. (weniger Symmetrie, mehr Kombinatorik)
siehe Penroseparkettierungen und Quasikristalle (5er und 10er Strukturen).
8-Eck und 12-Eck sind außer dem 3-, 4-, und 6-Eck die einzigen Polygone, welche archimedische Parkettierungen zulassen. 8 und 12 sind die größten gemeinsamen Teiler von 24. Mehr noch:
Alle Teiler der Ziffer 24, also:
1, 2, 3, 4, 6, 8 und 12 entsprechen auch allen möglichen Polygonen in platonischen und archimedischen Parkettierungen!
Die Bedeutung der Ziffer 24 in der Primzahlverteilung wird hier beschrieben.
Noch einmal das 12-Eck:
Die Ziffer 12 ist 1-, 2-, 3-, 4-, und 6-teilbar. Dies entspricht allen möglichen Drehungen von Symmetriegruppen periodischer Parkettierungen
also: 360°, 180°, 120°, 90° und/oder 60°
Die Ziffer 12 ist die letzte Zahl oberhalb der Teilbarkeitssumme von 2, die folgende Teilbarkeiskonstellation nicht aufweist:
|
|
Natürliche Zahl, ist mit dem betreffenden Teiler nicht teilbar, hat aber mit ihm mindestens einen gemeinsamen Teiler größer als eins.
Analog zur Geometrie der Simplexe:
Das 12-Eck-Simplex ist das letzte, welches – eben analog zu dieser arithmetischen Besonderheit – kein Sternpolygon aufweist, das aus Sternpolygonen zusammengesetzt ist. (Mit Ausnahme aller primzahligen Simplexe!)
Das 10-Eck-Simplex wiederum ist das erste Simplex oberhalb dem Teilbarkeitsergebnis 2,
bei dem diese Konstellation auftritt (10 geteilt
durch 4 = 2,5, gemeinsamer Teiler ist 2).
Bezieht man nämlich alle Ziffern und alle Teilbarkeitssummen unterhalb von 2 in diese Überlegungen mit ein, dann tritt diese Teilbarkeitskonstellation zum ersten Mal bei 6:4 bzw. 4:6 auf. Eine meiner Meinung nach sehr auffällige Übereinstimmung.
Denn nur 4- und 6-Eck sind mit sich selbst parkettierbar, wenn man davon ausgeht, dass
das 6-Eck ja schon 3-Ecke enthält.
Und hier ist eben wieder interessant, dass Dreiecke innerhalb einer Parkettierung immer zu einer Hälfte um 180 Grad gedreht sein müssen.
Zusammenfassend lässt sich also feststellen, dass die platonische und archimedische Parkettierbarkeit von Polygonen auffällige Übereinstimmungen in der Zahlentheorie aufweist.
|
|
 |
|
 |
|
Somit ist das Hexagon kein 3. Prinzip,
sondern ist in der Struktur von Dreiecken
schon enthalten.
Andererseits:
Die Pflasterbarkeit des Dreiecks funktioniert
nur im Wechsel aufrechter und gestürzter
Figuren.
Arithmetisch und philosophisch betrachtet
sind genau diese Sachverhalte äußerst
wichtig und interessant.
Denn:
2 Dreiecke mit einer Winkelsumme von je einem halben Kreis ergänzen sich zu einem vollen Kreis, dem 7. Kreis in der Mitte!
Alle Kreisanteile im Hexagon ergeben
3 Vollkreise.
Betrachtet man dagegen das hexagonale Gitter als archimedische Parkettierung von Sechssternen (Hexagrammen), dann hat jedes Hexagramm (das sich ja aus 2 Dreiecken zusammensetzt) eine Winkelsumme von genau einem vollen Kreis.
Das Quadrat ist dagegen das einzige Polygon, dessen vier Innenwinkel einen Vollkreis
ergeben.
Ich habe die Darstellung dieser Grafik animiert, um den Betrachter eben dazu zu animieren, diese Gesetzmäßigkeiten länger auf sich wirken zu lassen.
Die Schlichtheit dieser Struktur könnte nämlich zu der Annahme verleiten, dass ein kurzer Blick genügt.
|
|
Betrachten wir uns nun eine interessante
Gesetzmäßigkeit, die in der Kristallographie von
größter Bedeutung ist. Es geht dabei um
molekulare Strukturtypen, den Kristallgittern von
so genannten Kugelpackungen.
Projiziert man diese Packungsschemen vom Raum auf eine Ebene, so gibt es nur zwei reguläre Möglichkeiten, gleich große Kreise so aneinander zu ordnen, dass sie sich gegenseitig berühren:
1. die lockere gepackte Variante
2. dichtestgepackte Variante.
Es gibt nur diese beiden Möglichkeiten gleich
große Kreise regelmäßig so zu ordnen, dass
sie sich gegenseitig berühren.
|
|
Verbindet man die Mittelpunkte der Kreise,
so entstehen – je nach Schema – jeweils entweder Quadrate oder Dreiecke.
Die Struktur mit den dichter gepackten Kreisen
wird auch das hexagonale Gitter genannt, da sich
um den Mittelpunkt eines Kreises genau 6 Kreise
ordnen. Die rechts stehende Abbildung zeigt es.
Wir sehen:
Diese zwei Möglichkeiten von Kreisrastern lassen alle drei möglichen Platonischen Parkettierungen entstehen!
Das Hexagon umschließt einen 7. Kreis,
und setzt sich lediglich aus 6 Dreiecken
zusammen.
|
|
 |
|
|
|
 |
|
|
Schauen wir uns noch einmal alle möglichen Teiler der Ziffer 24 an, welche auch allen möglichen Polygonen in platonischen und archimedischen Parkettierungen entsprechen: 1, 2, 3, 4, 6, 8, 12
Es gibt da eine kontinuierliche 4er-Ordnung:
Alle ersten vier natürlichen Zahlen 1, 2, 3, 4
sind als Polygone regulär parkettierbar.
Denn nicht nur 3- und 4-Eck, sondern auch
1- und 2-Eck, nämlich Punkt und Linie sind Teil
einer regulären Parkettierung.
Bei den zweiten Vierergruppe 5, 6, 7, 8 ist es
nur noch jedes zweite, nämlich 6- und 8-Eck.
Bei der dritten Vierergruppe 9, 10, 11, 12 ist es
nur noch das vierte, nämlich das 12-Eck!
Also drei (3) 4er Gruppen!
Auch in der lückenlosen Parkettierung des dreidimensionalen Raumes sind genau diese Teiler der Ziffer 24: 1, 2, 3, 4, 6, 8, 12 strukturbildend.
Der Raum ist nur mit Tetraedern und Oktaedern im Verbund oder mit Hexaedern allein lückenlos parkettierbar.
Tetraeder: 4 Flächen (3-Ecke), 4 Ecken, 6 Kanten
Oktaeder: 8 Flächen (3-Ecke), 6 Ecken, 12 Kanten
Hexaeder: 6 Flächen (4-Ecke), 8 Ecken, 12 Kanten
Alternativ sind auch Parkettierungen mit den entsprechenden archimedischen Körpern möglich (abgestupfte Tetraeder, Oktaeder, Hexaeder),
die 6- und 8-eckige Flächen enthalten.
Betrachtet man aber nur die Kristallgitter von Kugelpackunsschemen, dann sind auch im 3-dimensionalen Raum nur Parkettierungen von Dreiecken und Quadraten möglich.
|
Die animierten Abbildungen in der Mitte zeigen dieses Kristallgitter in zwei verschiednen Ansichten.
Oben zu sehen ein Tetraeder, also eine Pyramide mit dreieckigem Grundriss und darunter ein halbes Oktaeder, eine Pyramide mit quadratischem Grundriss.
Beide Figuren sind Teil ein und der selben Struktur, nur in einer jeweils anderen Seitenansicht.
Wenn man diese Matrix nicht kennt, ist sie erst mal sehr verwirrend. Ich persönlich empfehle jedem, der sich für diese Struktur interessiert, sie selbst als Modell nachzubauen, um sie besser be-greifen zu können.
Es handelt sich dabei um das Kristallgitter der kubisch flächenzentrierten Kugelpackung, der Keplerschen Kugelpackung.
Diese wurde auch bekannt unter dem Namen: :
Buckminster Fullers isotrope Vektorenmatrix.
Sie ist als ein echtes Fraktal zu betrachten.
Die Lücken dieser schönsten (symmetrisch perfektesten) aller Kugelpackungen setzen sich immer wechselweise zusammen aus Oktaedern und Tetraedern.
Die roten Figuren sind Tetraeder,
die blauen Figuren sind Oktaeder.
Johannes Kepler war der erste, der diese Zusammenhänge nachweislich erkannte.
In wieweit die lückenlose Parkettierung des
Raumes tatsächlich mit der Kugelform, mit
der Ziffer 24 und vor allem auch mit der
Tetraktys zu tun hat, soll in der nächsten
Rubrik
DIE GEOMETRIE DER LÜCKENLOSEN RAUMFÜLLUNG
gezeigt werden.
|
|
 |
|
 |
|
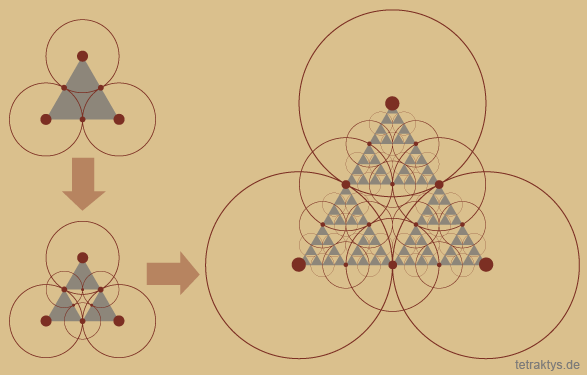
Modell einer "Schöpfungsmatrix"
Die rechts stehende Abbildung zeigt, wie an den "Sollbruchstellen" sich berührender Kreise eine fraktale Struktur entstehen kann.
Die Ecken der dabei entstehenden halbierten Kristallstrukturen bilden wieder die Mittelpunkte eines Kreisrasters mit dem entsprechend halben Durchmesser. Das gleiche Schema ist auch bei einer quadratischen Struktur möglich.
Demzufolge funktioniert diese interessante "fraktale Kettenreaktion" auch mit dem kubisch flächen-
zentrieren Gittermodell, welches oben beschrieben wurde.
Ab dem 5-Eck ist diese schöne wechselwirkende Matrix zwischen Kreisen bzw. Kugeln und Gitterstruktur zumindest im dreidimensionalen Raum nicht mehr möglich.
^ Zurück nach oben zum Menü ^
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|