|
|
|
|
|
|
|
|
 |
|
Bitte zuvor lesen:
DIVISIONSTABELLE & SIEB DES ERATOSTHENES
Figurierte Zahlenbrüche, Symmetrie und Asymmetrie der Primzahlen
Im Folgenden wollen wir uns einen weitere interessante Sichtweise zu eigen machen, wie diese "regelmäßige Unregelmäßigkeit" im Muster der Matrix des Zahlenlambdomas entsteht.
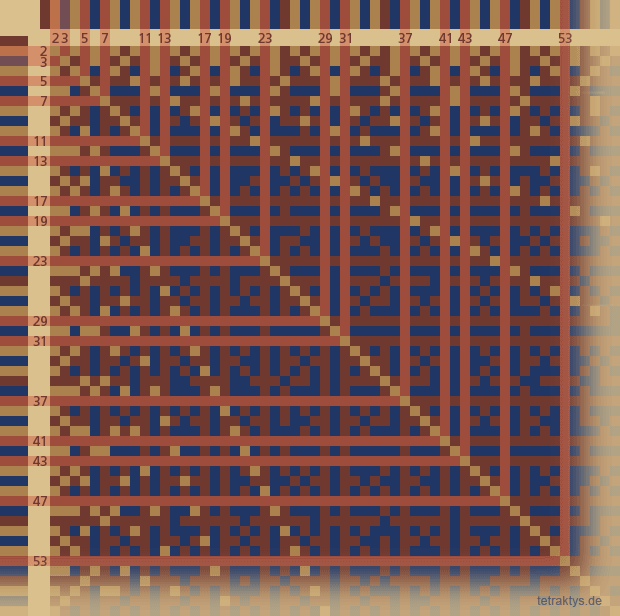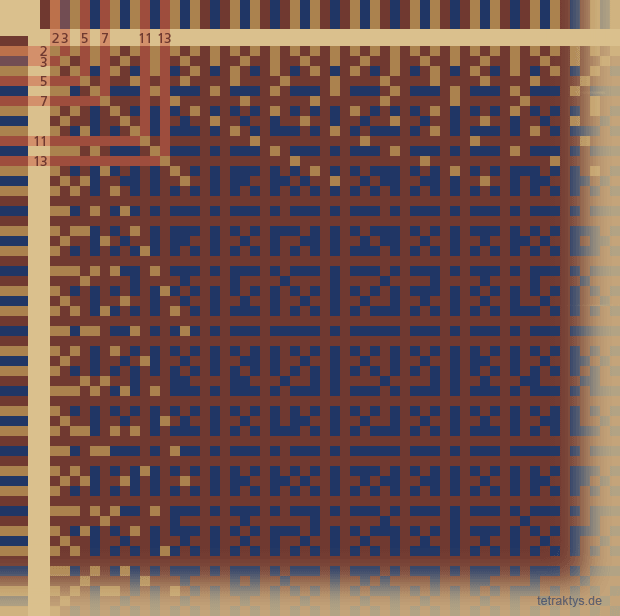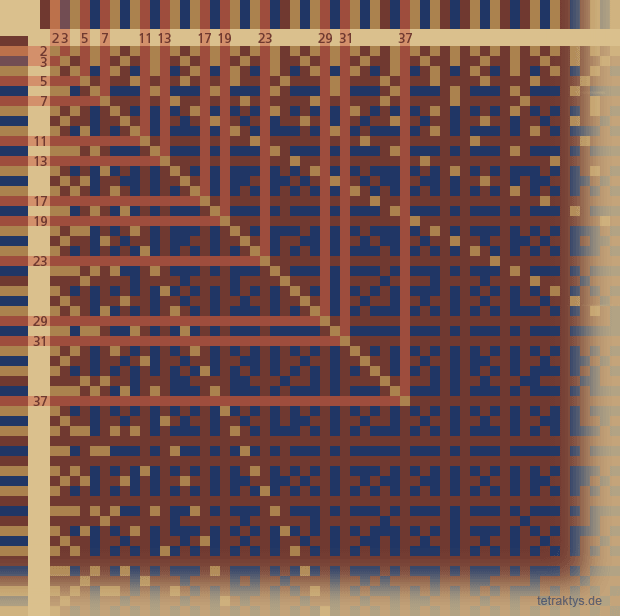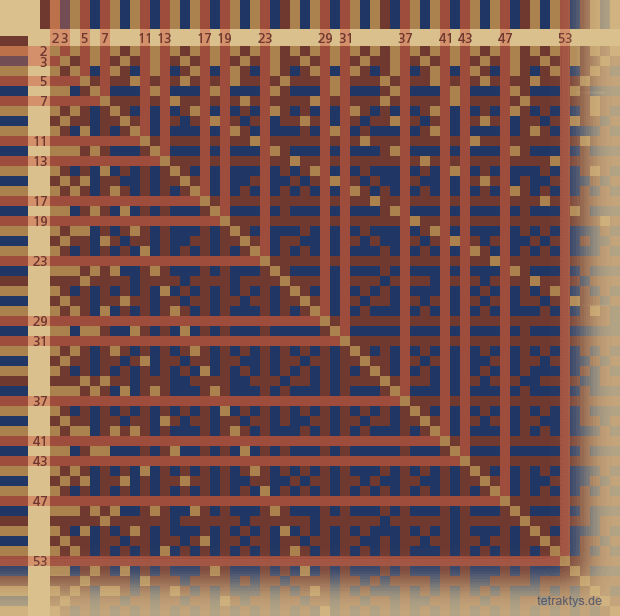
Die Abbildung rechts zeigt nun das Sieb des Eratonsthenes so, wie es vermutlich auch die Pythagoreer erkannt haben.
Nur die Primzahlen sind als hellrote Balken hervorgehoben, weil sie diese Matrix auch komplett abdecken.
Die gelben Pixel entsprechen dem uns
bekannten Sieb des Eratosthens, wogegen
die blauen Pixel diejenigen Positionen in
Koordinatensystem anzeigen, bei dem es
einen gemeinsamen Teiler mit dem jeweils
anderen Zahlenstrahl gibt.
Noch einmal:
Man muss sich immer bewusst sein, dass
sich der Zähler- und Nenner-Zahlenstrahl gleichwertig gegenüber stehen und prinzipiell beliebig austauschbar sind!
Erst dann kann man sich auch darüber
im Klaren sein, dass die erste Ursache der
Tetraktys = Vierheit in den geraden und ungeraden Zahlen sowohl im Zähler- als
auch im Nenner-Zahlenstrahl verortet ist!
Und der daraus resultierende "Doppelungs-
effekt" muss sich zwangsläufig in den entsprechenden Quotienten-Positionen des Koordinatensystems manifestieren.
|
|
|
 |
|
In dieser Animation sind die gleichen primitiven Punkteraster wie oben zu sehen – nur aufkumuliert und die Primzahlen wieder als rote Balken dargestellt. Denn alle anderen nicht primen Zahlen "erzeugen" die Matrix ja nicht, sondern sind schon in ihr enthalten.
Wenn man ein wenig über dieses Muster nachdenkt, dann muss man zu dem Schluss kommen, dass es sich hier in der Tat um figurierte Zahlen (bzw. figurierte Zahlenbrüche) handelt, genau wie das
10-Punkte-Dreieck der Pythagoreer.
Der vermutlich wichtigste Grund, warum die Pythagoreer von figurierten Zahlen so angetan waren, war zweifellos die Tatsache, dass diese Anordnungen von Zählsteinchen ganz ohne Zählsystem auskommen.
Warum ist das wichtig?
Unser Dezimalsystem ist ein Menschen gemachtes System! Die Dezimalschritte unseres Zählsystems versperren die Sicht auf das "Wesen der Zahl".
Denn sobald man sich innerhalb eines Zählsystems bewegt, muss man konsequenterweise fragen, welche Gesetzmäßigkeiten in andern Zählsystemen gelten.
Bei einem Punktemuster muss man nun nicht
mehr zählen:
1-2-3-4...bis 10 und dann in Dezimalschritten 20...30...40 usw..., sondern man könnte so zählen, als ob einem Zahlen fremd sind,
in der Art: hm, hm hm, hm..... so wie hochentwickelte Säugetiere, beispielsweise Delphine oder Affen oder eben auch Kleinkinder.
Fazit: Zahlentheorie ist eigentlich
schon Geometrie.
Wenn wir die Geometrie der Simplexe in
unsere Betrachtungen einbeziehen, wird
das noch viel deutlicher.
|
|
|
|
 |
|
|
 |
|
Mit diesem Punktemuster haben wir – salopp gesagt – figurierte Zahlenbrüche vor uns.
Und:
Auch das Sieb des Eratosthenes funktioniert unabhängig von einem Zählsystem wie dem Dezimalsystem.
Die komplette Matrix löst sich schließlich im Sieb des Eratosthenes auf.
(animierte, hellrot markierte Balken mit den ensprechend gekennzeichneten Primzahlen).
Alle primen Teilbarkeitskonstellationen
und natürlich auch die Primzahlen selbst
sind der Rest des rot-braunen Hintergrundes,
welcher der Zahl 1 entspricht.
Nun kann man auch nachvollziehen,
warum für die Pythagoreer die Ziffer 1
eigentlich gar keine Zahl war! Sie ist der
Urgrund, die Basis.
Achten Sie nun auf die ersten Raster, also
die Primzahlen 2, 3 und 5 in rechts stehender Animation.
Die Primzahlen 2 und 3 ergänzen sich zu
einem perfekt symmetrischen Muster.
Dieses Muster ist – wie man unschwer
erkennen kann – die Basis für die
Primzahlzwillingsbildung!
Sie bilden das Grundgerüst für die "Primzahlkanäle" des 6er Zwillingstaktes.
Die Zahl 4 geht in der Primzahl 2 auf.
Die Ziffern 1 + 2 + 3 + 4 sichern also den 6er Takt ab.
Ab der Primzahl 5 werden aber nun die "Primzahlkanäle" systematisch wieder "verstopft".
Denn das Quadrat der Ziffer 5 = 25 ist
die erste Pseudoprimzahl, welche die
geschlossene Primzahlzwillingsbildung
auflöst.
Schauen Sie sich die Animation bitte
länger an um sie zu verstehen.
Philosophisch betrachtet ist es die Ziffer 3,
welche die Gegensätze versöhnt, die geraden
und ungeraden Zahlen, das aktive und passive,
männlich und weiblich zu einer 6-teiligen
Ordnung zusammenfügt. Das ist nicht nur Zahlenmystik, sondern auch die Wahrheit.
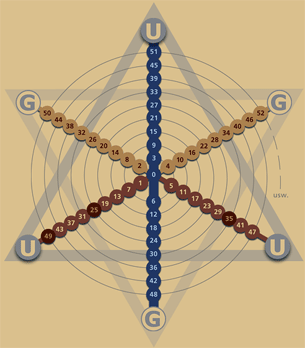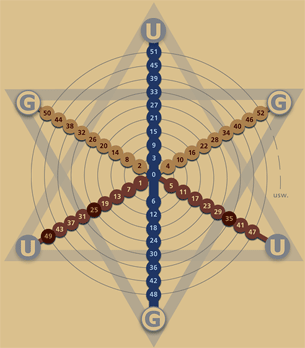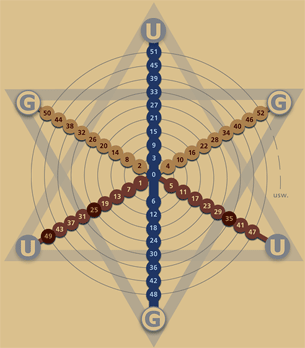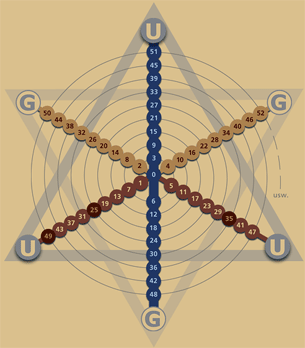
Die rechts stehende Abbildung zeigt eine Zahlenspirale in einer 6er-Steigung um diesen Sachverhalt ebenfalls zu verdeutlichen:
Die Buchstaben "U" kennzeichnen die ungeraden Zahlen, die Buchstaben "G" die geraden Zahlen. Betrachten Sie diese Grafik in Großansicht gegebenenfalls noch einmal unter:
TETRAKTYS PART 1
– DIE ORDNUNG DER PRIMZAHLEN
Über die "besonderen Primzahlen" 1, 2 und 3
habe ich in diesem zweiten Teil der Rubrik "Zahlentheorie" schon ausgiebig geschrieben.
|
|
|
|
|
|
 |
|
 |
|
|
|
Auch dieser Sechsstern zeigt, wie der aus
dieser Dreiheit resultierende 6er Takt,
die Matrix für alle weiteren Primzahlplätze
bis unendlich festlegt.
Dieser Sachverhalt war mit Sicherheit ein entscheidener Punkt, der die Philosophen der Antike beeindruckt und beeinflusst hat.
Schon der Pythagoreer Philolaos hat vor 2500 Jahren das harmonisierende Prinzip der Ziffer Drei gelobt.
Auch die geistigen Nachfahren der Pythagoreer,
die Freimauer, verehren heute noch die ihnen
heilige Zahl 3.
Möglicherweise sind daraus auch die Religions-
philosophien des jüdisch, christlichen
Abendlandes entstanden:
Die Trinität Gottes und seine Schöpfung der Welt in 6 Tagen...
|
|
 |
|
Dabei ist nun noch etwas interessant:
Bereits zweimal bin ich darauf hingewiesen
worden, dass diese Matrix sehr an hebräische Druckbuchstaben erinnert. Nun wird die hebräische Quadratschrift auch "Sprache Gottes" genannt.
In Wikipedia kann man nachlesen, dass im zweiten Jahrhundert n. Chr. von den jüdischen religiösen Autoritäten das Althebräisch von der Quadratschrift abgelöst wurde, da diese für religiöse Texte geeigneter sei.
Auch die mittelalterlichen Magier bedienten sich
der hebräischen Quadratschrift, um als "Schöpfergott" etwas bewirken zu wollen oder zu können. Sie bedienten sich nicht nur der "Sprache Gottes" sondern verwendeten für ihre magischen Symbole auch Sternpolygone, wie das Hexagramm oder Pentagramm.
|
|
|
|
|
|
|
 |
Simplexe enthalten Sternpolygone, und ihre
Auffächerung in die Divisionstabelle erzeugen
exakt die selbe Matrix.
Dies alles gibt meiner Meinung nach berechtigten Anlass für Spekulationen.
Zumindest deutet das alles darauf hin, dass diese Matrix der Divisionstabelle schon sehr lange bekannt ist, bzw. bekannt war.
Um so erstaunlicher ist, dass dieses "Schöpfungsmuster" in der Weise wie ich es hier gezeigt habe, heutzutage kaum einer kennt.
Eine kleine Abhandlung gibt es auf der Seite von Pythagoras-Institut. Ansonsten habe ich dieses Muster außer eben in vereinfachter Form auf divisorplot.com nirgendwo im Internet finden können.
|
|
| Amulett aus Sternpolygonen auf hebräischer Quadratschrift. |
|
 |
|
|
Aber zurück zur Matrix selbst:
Zusammenfassend muss man also feststellen, dass mit dem Raster der Ziffer 4 diese perfekte Symmetrie abgeschlossen ist.
Betrachtet man nun das Lambdoma wieder
um 45 Grad gekippt und bezieht die
Zahlenbrüche der beiden n-Stahlen mit ein,
so wie ganz oben dargestellt, so beschreibt
an der Spitze des Koordinatensystems der
Divisionstabelle, bzw. des Lambdomas
das 10-Punkte-Dreieck der Pythagoreer
diesen Sachverhalt.
Dieses 10-Punkte-Dreieck wird uns an allen Ecken und Enden der Divisionstabelle begegnen, genau da, wo eine neue Ordnung beginnt und eine alte Ordnung endet.
Sonst ergäbe dieses 4er-10er-Intervall ja auch keinen Sinn, bzw. wäre nicht als solches erkennbar. Denn die Pythagoreische Tetraktys
ist ein hierarchisches System.
|
|
|
|
 |
|
|
 |
|
 |
|
|
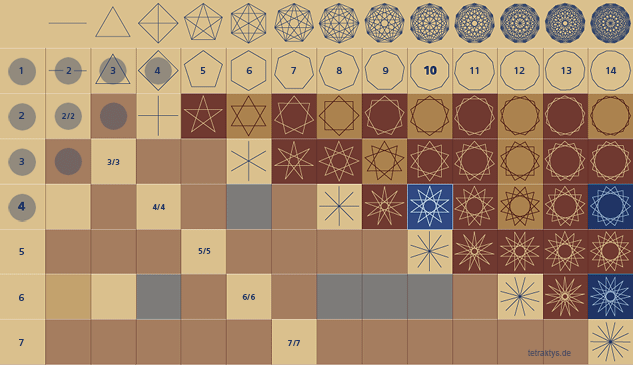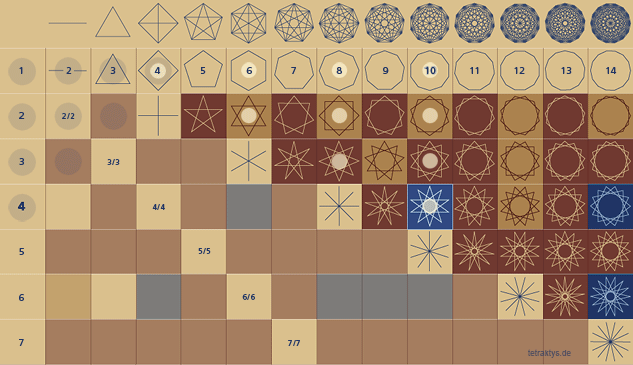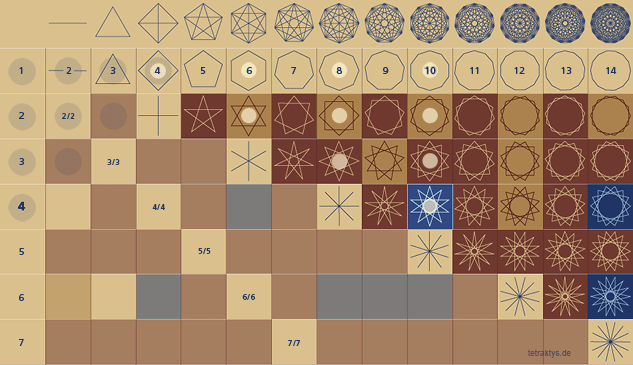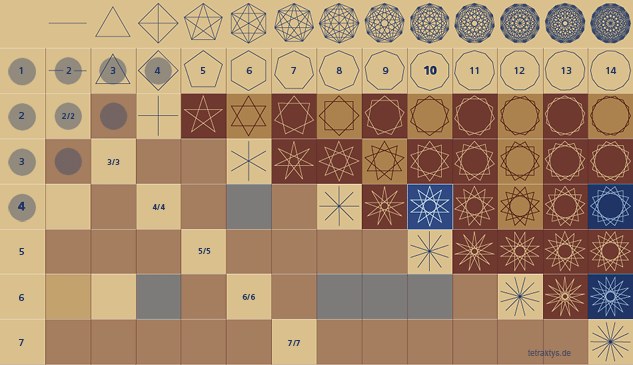
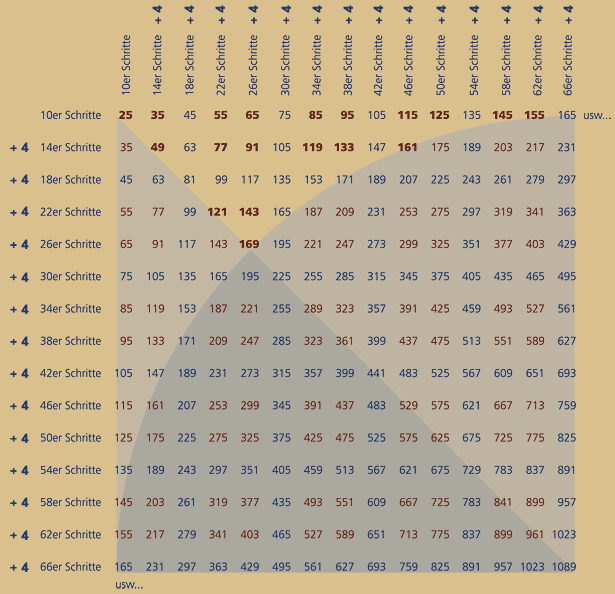
Rechts stehende Tabelle war im Jahre 2010 ein Versuch, Zusammenhänge zwischen der Tetraktys und dem Sieb des Eratosthenes nicht mit Punkten sondern mit Ziffern zu zeigen.
Leider ist diese Darstellung nicht leicht
zu verstehen, sie zeigt keine Primzahlen, sondern alle lückenlos gestrichenen Primzahlplätze der Form 6n±1 rotbraun und fett markiert, ab der Zahl 25 bis 169:
10er Schritte ab 25 = 5 x 5
14er Schritte ab 35 = 5 x 7
18er Schritte ab 45 = 5 x 9
22er Schritte ab 55 = 5 x 11
26er Schritte ab 65 = 5 x 13
30er Schritte ab 75 = 5 x 15
34er Schritte ab 85 = 5 x 17
38er Schritte ab 95 = 5 x 19 u.s.w...
Um die Ordnung des Systems zu verstehen,
sind alle ungeraden Zahlen enthalten, also auch
3-teilbare Zahlen außerhalb der potenziellen
Primzahlzwillingsplätze – blau markiert.
Was obige Tabelle noch zeigt:
Das Dreieck deckt die spiegelsymmetrisch angeordneten “doppelten Lottchen” ab.
Der viertel Kreisbogen deckt diejenigen Zahlen ab, welche aus Platzgründen hier unvollständig angezeigt sind.
Nur die fettgedruckten roten Zahlen im frei
bleibenden Bereich sind lückenlos bis zur Zahl
169 aufgelistete gestrichene Primzahlplätze
aus 6n±1.
Die dreiteilbaren Zahlen sind blau markiert und
bilden die determinierenden Symmetrieachsen,
wenn man die komplette Divisionstabelle
betrachten würde.
|
|
|
|
 |
|
 |
|
|
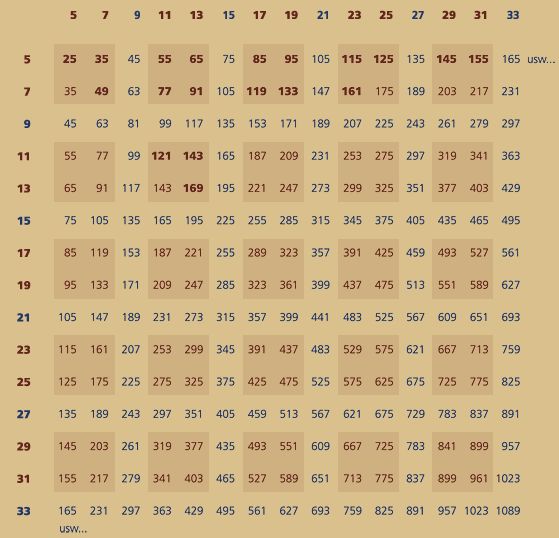
Die rechts stehende Tabelle zeigt im Prinzip das selbe Schema wie die obere Tabelle, nur mit dem Unterschied, dass hier die Koordinaten die entsprechenden rot markierten Primzahlen anzeigen, deren Vielfache bzw. Pseudoprimzahlen sich in der Tabelle befinden.
Wenn man die Postitionen dieser Pseudoprimzahlen wieder in der normalen Divisionstabelle betrachtent würde, in der alle Zahlenbrüche enthalten sind, dann stellt man eben fest, dass oberhalb von Teiler 2 diese Intervalle immer um 10 versetzt beginnen!
Denn logischerweise hat das Sieb des Eratosthenes nur oberhalb von Teiler 2 eine Relevanz!
10er Folge: 25, 35, 45, 55, 65, 75, 85, 95...
4er Abfolge: 10, 14, 18, 22, 26, 30, 34, 38...
Da sich Zähler und Nenner gegenseitig bedingen, ist das System zumindest für einen Laien schwer zu durchschauen.
Diese Ordnung immer um 10 und 4 versetzter Raster
im Koorinatensystem muss sich bis unendlich
fortsetzen, da dies eben dem SdE entspricht.
Sie ist auch die Konsequenz aus der Pythagoreischen Tetraktys, welche diese sich überlagernden Raster entstehen lässt und die daraus resultierend, eine scheinbar chaotische Primzahlverteilung zeigt.
Und es muss auch nicht verwundern, wenn sich hier zwei ehrenwerte Griechen, Pythagoras und Eratosthenes ein Stelldichein geben. (Eratosthenes war Platoniker).
Diese Ordnung zeigen auch die Sternpolygone der Simplexe, wenn man diese in ein Koordinatensystem auffächert.
SIMPLEXE & PRIMZAHLEN IN DER DIVISIONSTABELLE
|
|
 |
|
 |
|
|
|
Hier nun etwas entfernt Ähnliches:
"Die 4 Primzahlen-Temperamenten" vom
Kommunikationskünstler Felix Stoffel.
Wobei diese Erkenntnisse nicht neu sind.
Zum Theorem:
Man versucht, in der "rätselhaften" Verteilung der
Primzahlen doch Regelmäßigkeiten zu entdecken,
das große Thema aller Primzahlforscher.
Geht man nun auf die Suche nach Primzahlen – Gauß tat das oft »im Kopf« bei seinen ihm manchmal langweiligen Vermessungsarbeiten –,
so stellt man leicht fest, dass gerade Zahlen (außer 2 selbst) keine Primzahlen sein können, ebenso wenig Zahlen, die auf 5 enden (wieder außer 5 selbst).
|
|
Bleiben also nur Zahlen mit den Endziffern 1, 3, 7 und 9. Diese sind manchmal Primzahlen, manchmal nicht.
Dirichlet hat darüber bewiesen: Auf lange Sicht verteilen sich die unendlich vielen Primzahlen völlig gleichmäßig auf die 4 möglichen Typen.
Es kommt aber noch besser:
Wenn man die letzten zwei Endziffern
einer Zahl berücksichtigt, also von 01, 03, ...
bis 99, so gibt es 40 mögliche Typen, und
wieder herrscht gleichmäßige Verteilung.
Geht man noch weiter zu drei Endziffern,
so gibt es 400 gleichmäßig besetzte Typen
– und so fort.
|
|
Es mag einem schwindlig werden, aber
so ist es, Dirichlet hat es bewiesen.
Und, wie schon Kästner betont hat,
da gibt es dann keine Diskussion mehr.
Diese Gesetzmäßigkeiten beschränken sich allerdings nur auf unser Dezimalsystem.
Siehe Wikipedia:
Dirichletscher Primzahlsatz
Die Zusammenhänge rund um die Tetraktys
regen aber dazu an, über diesen Dirichletschen Primzahlsatz neu nachzudenken.
|
|
 |
|
|
|
Weiter geht es unter: SIMPLEXE & PRIMZAHLEN IN DER DIVISIONSTABELLE
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|